プログラミングを行う上で考慮したいコンピュータ内の制御
医療ソリューション事業部のKISHIです。初めましての人は初めまして。

先月、かのLinus氏(★1.2)がIntelのSpectore/Meltdownに関するパッチについて(★3)、公開メーリングリストでかなり辛辣な言葉を吐いていたのが話題でしたね。
私も、以前の職場での出来事が重なってしまったものです。
(★1) Linus氏= Linuxの生みの親であるリーナス・トーバルズ氏
(★2) Linuxとは=UNIXとは異なりゼロから開発されたOSではあるがUNIXの標準仕様に準拠しているためUNIX系OSと呼ばれている
(★3)公開メーリングリスト https://lkml.iu.edu/hypermail/linux/kernel/1801.2/04628.html
Spectore/Meltdownに関するパッチについての記事
https://jp.techcrunch.com/2018/01/23/2018-01-22-linus-torvalds-declares-intel-fix-for-meltdown-spectre-complete-and-utter-garbage/
テーマ:「実数を扱う」
さておき今回は、プログラミングを行う上で考慮したいコンピュータ内の制御について基礎的なお話をさせて頂きます。
具体的なテーマは・・「実数を扱う」です。。ニッチですね。
特別な設定やインストールの必要のない、手軽に試せるjavascript先生を例にしてやってみたいと思います。
但しプログラミング言語については、主要な言語(C++やR言語等‥)で扱えるものであれば大体なんでもいいでしょう。
「0.5-0.4」という計算の仮定
では、Javascript先生に「0.5-0.4」という算数の計算をやってもらい、答え合わせをして頂きます。
テキストエディタなどでこちらの文をコピーし、張り付けてみます。
—————————————————————————
<!DOCTYPE html>
<html lang=”ja”><head><meta charset=”utf-8″><title>答えは0.1</title></head>
<body>
<script>
// 変数aとbにそれぞれ0.5、0.4を代入し、cには0.5、0.4を計算した結果を代入します。
var a = 0.5;
// ※1… 1を足して1を引いているのはおまじないのようなものです。のちに説明します。
var b = 0.4 + 1 – 1;
var c = a – b;
// 答えは0.1であります。
var z = 0.1;
document.write(“(1)”);
// cとzが同じ値であれば画面にtrueと表示され、違えばfalseと表示されます
if (c == z) document.write(“true”);
else document.write(“false”);
document.write(“<br/>(2) a=” + a + “の2進数の値:<br/> ” + a.toString(2));
document.write(“<br/>(3) b=” + b + “の2進数の値:<br/> ” + b.toString(2));
document.write(“<br/>(4) c=” + c + “の2進数の値:<br/> ” + c.toString(2));
document.write(“<br/>(5) z=” + z + “の2進数の値:<br/> ” + z.toString(2));
document.write(“<br/>(6) z + 1.0 – 1.0 の値(2進):<br/> ” + (z+1-1).toString(2));
document.write(“<br/>(7) z + 1.0 – 1.0 の値(10進):<br/> ” + (z+1-1));
</script>
</body></html>
—————————————————————————
では、このファイルを「sample.html」という名前で保存し、ウェブブラウザで開きます。
ファイル内にも書いてありますが、(1)ではaの0.5からbの0.4を引いた結果が0.1であれば「true」という文字列が返されます。
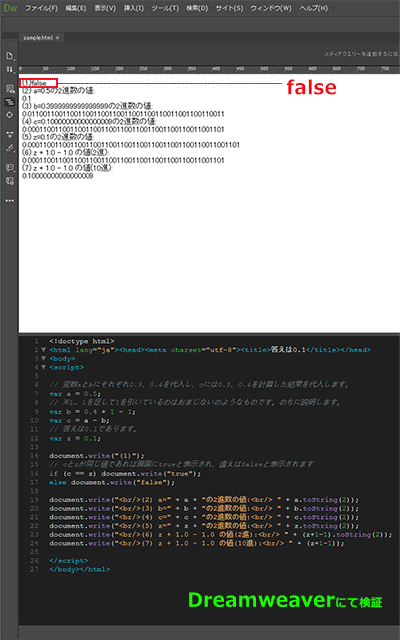
結果は「true」?
(1)の結果から見てきましょう。
「false」と返されてしまいます。
0.5-0.4は0.1で間違いはないはずなんですが…。小学校の算数をやり直さなきゃダメなのかな…。
こういう時は、コンピュータの気持ちになって考えるのです──。
コンピュータの演算処理では、信号中の電流の在り無しから2進数を表現して処理が行われます。
では手始めに、それぞれの変数を2進数で表現してみましょう。まずはaから。
(2)aは0.5、2進数では0.1です。
こちらは良いんです。
問題はここから。
(3)のbは0.4、2進数で表そうとするとこうなります。
0.0110011001100110011001100110..
小数点以下は「0110」を繰り返す循環小数となってしまいます。
当然、信号には限りがありますから、途中で途切れます。
それをまた10進数に直せば0.3999999999..となってしまいますね。
例えるなら1/3を小数では0.33333..の循環小数で表しきれないようなものです。
(4)の計算結果も当然誤差が生じています。。
一方、(5)変数zは0.1を2進数でどう見ているかというと
0.0001100110011001100110011001100110011001100110011001101
0.0001の後に1001を繰り返す循環小数になっていますが、最後のビットでに切り上げが行われていますね。
長くなってしまうので細かい話は割愛、これは10進数で出力すると0.1と表示してくれています。
「false」となる理由
ですが、ここで(4)に疑問が残ります。
何故、「0.4ではなく0.39999..と表示されたか?」です。
コード中の「※1」ではおまじないと称してbの変数の宣言で0.4+1-1と一見無駄なことをしていますが、1.0を足したことで、下の桁が2ビット減ってしまいます。で、1.0を引いて元の数値より2ビット少ない数値の出来上がりです。
※1と同じことをzに対して行うと、やはり(6)、(7)の様に桁が(5)よりも4ビット減っています。この辺りはjavascriptでの話ですが。
ついでに言うと、zに0.5を加減算すると2ビット消えるし、0.0625を加減算するときちんと元に戻ります。これを説明するといよいよ3時間番組になってしまいそうなので、やはり割愛します。
さらについでに言うと、※1で行ったおまじないは消しても、bの0.4の桁数が元よりzの0.1よりも桁数が2ビット小さく、結局cで0.1の値が表現しきれないので、答えはfalseとなります。
まとめ
いろいろ試すと本当に楽しいです。(私は)
どの言語でも、これらの計算を正確に行うための「機能」がどこかしらに用意されているのですが、自分で計算方法を編み出す方が楽しかったりします。
はっきり言って、全然意味なんて無いのですが。
そういったよくある計算機能を作らなければならない場面は、恐らく今の仕事では中々起こり得ないでしょう。ライブラリが限られる環境とか演算回路を作るとなれば、マイコン系のICとかFPGAの話ですから。
電子工作なんかをしている頃は、こういった2進数の信号処理・制御の話が目の前にある事なので避けては通れないのですが、ウェブやデスクトップアプリケーション開発だと、2進数を意識することが極端に減るような気がします。技術者としては、あまり良くないと感じることもあります。
次回と時間があったら、7.1セグメントLEDの表示器の制御についてでもお話ししたいと思います。(本当に趣味だけの話です)
以上、私が楽しいだけの算数のお話でした。

